Giao Điểm Của 3 Đường Trung Tuyến Trong Một Tam Giác Là Gì? Trọng Tâm [2025]

(mở bài)
Hiểu rõ về giao điểm của 3 đường trung tuyến trong tam giác không chỉ là Kiến thức toán học cơ bản, mà còn là nền tảng để giải quyết nhiều bài toán hình học phức tạp. Trong bài viết thuộc chuyên mục “Kiến thức” này, chúng ta sẽ cùng nhau khám phá định nghĩa chính xác về trọng tâm tam giác, cách xác định vị trí trọng tâm, các tính chất quan trọng liên quan đến trọng tâm và ứng dụng của nó trong các bài tập. Đặc biệt, bài viết sẽ đi sâu vào cách chứng minh giao điểm ba đường trung tuyến và các bài toán liên quan đến tỉ lệ đoạn thẳng được tạo bởi trọng tâm. Với những kiến thức này, bạn sẽ nắm vững kiến thức về trọng tâm và tự tin chinh phục mọi bài toán hình học.

Trọng tâm của tam giác: Giao điểm đường trung tuyến và ý nghĩa hình học

Giao điểm của 3 đường trung tuyến trong một tam giác, hay còn gọi là trọng tâm tam giác, là một điểm đặc biệt mang ý nghĩa quan trọng trong hình học. Điểm này không chỉ là giao điểm đơn thuần, mà còn thể hiện sự cân bằng và là tâm tỉ cự của ba đỉnh tam giác. Vị trí của trọng tâm luôn nằm bên trong tam giác, bất kể hình dạng của tam giác đó là gì.

Đường trung tuyến của một tam giác là đoạn thẳng nối một đỉnh của tam giác đến trung điểm của cạnh đối diện. Mỗi tam giác có ba đường trung tuyến, và ba đường này luôn đồng quy tại một điểm, điểm đó chính là trọng tâm. Ví dụ, trong tam giác ABC, nếu AM là đường trung tuyến kẻ từ đỉnh A đến trung điểm M của cạnh BC, thì trọng tâm G sẽ nằm trên đoạn AM.

Ý nghĩa hình học của trọng tâm không chỉ dừng lại ở giao điểm. Trọng tâm chia mỗi đường trung tuyến thành hai đoạn, trong đó đoạn nối từ đỉnh đến trọng tâm dài gấp đôi đoạn nối từ trọng tâm đến trung điểm cạnh đối diện. Cụ thể, nếu G là trọng tâm của tam giác ABC và AM là đường trung tuyến, thì AG = (2/3)AM và GM = (1/3)AM. Tính chất này vô cùng quan trọng trong các bài toán chứng minh và tính toán liên quan đến tam giác.

Tính chất quan trọng của giao điểm 3 đường trung tuyến trong tam giác

Giao điểm của 3 đường trung tuyến trong tam giác, hay còn gọi là trọng tâm tam giác, sở hữu những tính chất hình học đặc biệt quan trọng, đóng vai trò then chốt trong nhiều bài toán và ứng dụng thực tế. Các tính chất này không chỉ giúp giải quyết các bài toán liên quan đến tam giác một cách hiệu quả mà còn cung cấp những hiểu biết sâu sắc về cấu trúc và đặc điểm của hình học phẳng.

Một trong những tính chất quan trọng nhất của trọng tâm là nó chia mỗi đường trung tuyến thành hai đoạn theo tỉ lệ 2:1, tính từ đỉnh của tam giác đến trọng tâm. Ví dụ, nếu AM là một đường trung tuyến của tam giác ABC, và G là trọng tâm, thì AG = (2/3)AM và GM = (1/3)AM. Tỉ lệ này không chỉ đúng với một đường trung tuyến mà đúng với cả ba đường, tạo nên sự cân bằng và hài hòa trong cấu trúc tam giác. Điều này có nghĩa là, trọng tâm luôn nằm gần đỉnh hơn so với trung điểm cạnh đối diện.

Ngoài ra, trọng tâm của tam giác còn là điểm cân bằng vật lý của tam giác đó. Nếu ta coi tam giác như một tấm vật liệu đồng chất, trọng tâm chính là điểm mà ta có thể đặt ngón tay vào để giữ cho tam giác cân bằng hoàn hảo, không bị lật hay nghiêng. Tính chất này xuất phát từ việc trọng tâm là trung bình cộng vị trí của ba đỉnh tam giác, thể hiện sự phân bố đều về khối lượng.

Một tính chất khác liên quan đến diện tích, đó là ba đường trung tuyến chia tam giác thành sáu tam giác nhỏ có diện tích bằng nhau. Điều này có nghĩa là, nếu diện tích tam giác ABC là S, thì diện tích mỗi tam giác nhỏ tạo bởi các đường trung tuyến (ví dụ: tam giác AGB, BGC, CGA,…) sẽ là S/6. Tính chất này thường được sử dụng để giải các bài toán về diện tích tam giác một cách nhanh chóng và hiệu quả.

Cuối cùng, trọng tâm tam giác luôn nằm bên trong tam giác, bất kể hình dạng của tam giác đó là gì (nhọn, tù, hay vuông). Điều này giúp ta dễ dàng xác định vị trí tương đối của trọng tâm so với các yếu tố khác trong tam giác, cũng như so với các điểm đặc biệt khác như trực tâm, tâm đường tròn nội tiếp và ngoại tiếp (sẽ được đề cập chi tiết hơn ở các phần sau).

Cách xác định giao điểm 3 đường trung tuyến trong tam giác bằng phương pháp hình học

Để xác định giao điểm 3 đường trung tuyến hay còn gọi là trọng tâm của một tam giác bằng phương pháp hình học, chúng ta sẽ dựa vào tính chất cơ bản của đường trung tuyến và cách chúng giao nhau. Việc xác định giao điểm của 3 đường trung tuyến trong một tam giác là một kỹ năng quan trọng trong hình học, giúp giải quyết nhiều bài toán liên quan đến tính chất của tam giác.

Để xác định giao điểm 3 đường trung tuyến một cách trực quan và chính xác, bạn có thể thực hiện theo các bước sau:

1. Vẽ tam giác: Bắt đầu bằng cách vẽ một tam giác ABC bất kỳ trên giấy hoặc sử dụng phần mềm hình học. Tam giác này có thể là tam giác thường, tam giác cân, tam giác vuông, hoặc tam giác đều.

2. Xác định trung điểm: Tìm trung điểm của mỗi cạnh của tam giác. Trung điểm của cạnh AB là điểm M, trung điểm của cạnh BC là điểm N, và trung điểm của cạnh CA là điểm P. Bạn có thể sử dụng thước và compa để xác định trung điểm chính xác.

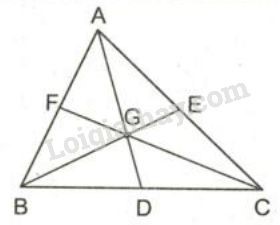
3. Vẽ đường trung tuyến: Vẽ đường trung tuyến từ mỗi đỉnh của tam giác đến trung điểm của cạnh đối diện. Đường trung tuyến từ đỉnh A đi qua điểm N, đường trung tuyến từ đỉnh B đi qua điểm P, và đường trung tuyến từ đỉnh C đi qua điểm M.

4. Xác định giao điểm: Ba đường trung tuyến này sẽ giao nhau tại một điểm duy nhất. Điểm này chính là trọng tâm G của tam giác ABC.

Lưu ý quan trọng:

• Bạn chỉ cần vẽ hai đường trung tuyến để xác định giao điểm. Đường trung tuyến thứ ba sẽ luôn đi qua điểm giao của hai đường trung tuyến đầu tiên. Điều này giúp bạn tiết kiệm thời gian và công sức khi vẽ hình.
• Trong trường hợp bạn sử dụng phần mềm hình học, phần mềm sẽ tự động xác định giao điểm khi bạn vẽ các đường trung tuyến.

Việc xác định trọng tâm bằng phương pháp hình học này không chỉ giúp bạn hiểu rõ hơn về tính chất của đường trung tuyến, mà còn là nền tảng để giải quyết các bài toán hình học phức tạp hơn liên quan đến tam giác. Ví dụ, bạn có thể sử dụng trọng tâm để chứng minh các định lý, tính diện tích, hoặc xác định vị trí tương đối của các điểm khác trong tam giác.

Cách tính tọa độ giao điểm 3 đường trung tuyến khi biết tọa độ đỉnh tam giác

Giao điểm của 3 đường trung tuyến trong một tam giác, hay còn gọi là trọng tâm, có thể dễ dàng xác định tọa độ khi biết tọa độ các đỉnh của tam giác đó. Việc này không chỉ là một bài toán hình học đơn thuần mà còn ứng dụng trong nhiều lĩnh vực khác. Công thức tính tọa độ trọng tâm dựa trên trung bình cộng tọa độ các đỉnh, thể hiện mối quan hệ đặc biệt giữa trọng tâm và các đỉnh của tam giác.

Để tính tọa độ trọng tâm G(xG, yG) của một tam giác ABC khi biết tọa độ các đỉnh A(xA, yA), B(xB, yB), và C(xC, yC), ta áp dụng công thức sau:

• xG = (xA + xB + xC) / 3
• yG = (yA + yB + yC) / 3

Công thức này xuất phát từ việc trọng tâm chia mỗi đường trung tuyến theo tỷ lệ 2:1, với khoảng cách từ đỉnh đến trọng tâm gấp đôi khoảng cách từ trọng tâm đến trung điểm cạnh đối diện. Ví dụ, nếu tam giác ABC có A(1, 2), B(4, 5), và C(7, 3), thì tọa độ trọng tâm G sẽ là:

• xG = (1 + 4 + 7) / 3 = 4
• yG = (2 + 5 + 3) / 3 = 10/3

Vậy, tọa độ trọng tâm G là (4, 10/3).

Như vậy, bằng cách áp dụng công thức đơn giản này, ta có thể dễ dàng xác định vị trí trọng tâm của tam giác chỉ với thông tin về tọa độ các đỉnh. Phương pháp này không chỉ hữu ích trong giải toán hình học mà còn trong các ứng dụng thực tế liên quan đến đồ họa máy tính, thiết kế kỹ thuật và nhiều lĩnh vực khác.

Ứng dụng của giao điểm 3 đường trung tuyến trong giải toán hình học phẳng

Trong giải toán hình học phẳng, giao điểm của 3 đường trung tuyến, hay còn gọi là trọng tâm tam giác, đóng vai trò như một công cụ mạnh mẽ để giải quyết nhiều bài toán khác nhau. Trọng tâm tam giác không chỉ là một điểm đặc biệt mà còn mang nhiều tính chất hữu ích, giúp đơn giản hóa các chứng minh và tính toán phức tạp.

Một trong những ứng dụng quan trọng nhất của trọng tâm là trong việc chứng minh các đường thẳng đồng quy. Nếu ba đường thẳng nào đó cắt nhau tại một điểm duy nhất, và điểm đó trùng với trọng tâm của một tam giác liên quan, thì ta có thể kết luận rằng ba đường thẳng đó đồng quy. Điều này xuất phát từ tính chất cơ bản của giao điểm 3 đường trung tuyến – điểm này luôn nằm trên cả ba đường trung tuyến. Ví dụ, khi chứng minh một đường thẳng đi qua trung điểm của một đoạn thẳng và đồng thời đi qua trọng tâm của một tam giác, ta có thể suy ra đường thẳng đó là một trong ba đường trung tuyến của tam giác đó.

Ngoài ra, giao điểm 3 đường trung tuyến còn được sử dụng để giải các bài toán liên quan đến diện tích. Trọng tâm chia tam giác thành ba tam giác nhỏ có diện tích bằng nhau. Điều này giúp chúng ta tính toán diện tích một cách dễ dàng hơn trong nhiều trường hợp. Chẳng hạn, nếu biết diện tích của một tam giác và vị trí trọng tâm, ta có thể suy ra diện tích của mỗi tam giác nhỏ được tạo thành.

Ứng dụng khác nằm trong các bài toán dựng hình. Việc xác định trọng tâm giúp chúng ta dựng các yếu tố khác của tam giác, ví dụ như dựng các đường trung tuyến còn lại khi biết một đường trung tuyến và trọng tâm. Hơn nữa, tính chất giao điểm 3 đường trung tuyến chia mỗi đường trung tuyến thành hai đoạn, trong đó đoạn nối từ đỉnh đến trọng tâm bằng 2/3 độ dài đường trung tuyến, giúp giải quyết các bài toán liên quan đến tỷ lệ đoạn thẳng.

Giao điểm đường trung tuyến so với các điểm đặc biệt khác trong tam giác (trực tâm, tâm đường tròn nội tiếp, ngoại tiếp)

Giao điểm của 3 đường trung tuyến trong một tam giác, hay còn gọi là trọng tâm, là một điểm đặc biệt, nhưng nó khác biệt hoàn toàn so với các điểm đặc biệt khác như trực tâm, tâm đường tròn nội tiếp và tâm đường tròn ngoại tiếp. Mỗi điểm này có một định nghĩa và tính chất hình học riêng, và vị trí của chúng thường không trùng nhau, trừ một số trường hợp đặc biệt của tam giác.

Trực tâm là giao điểm của ba đường cao trong tam giác. Trong khi trọng tâm liên quan đến sự cân bằng và chia tỉ lệ các cạnh, trực tâm lại liên quan đến tính vuông góc và độ cao của tam giác. Vị trí của trực tâm phụ thuộc vào dạng của tam giác: nằm trong tam giác nhọn, trùng với đỉnh góc vuông của tam giác vuông, và nằm ngoài tam giác tù. Mối liên hệ giữa trọng tâm và trực tâm thể hiện rõ nhất qua đường thẳng Euler, đường thẳng này đi qua trọng tâm, trực tâm, và tâm đường tròn ngoại tiếp.

Tâm đường tròn nội tiếp là giao điểm của ba đường phân giác trong của tam giác. Điểm này cách đều ba cạnh của tam giác và là tâm của đường tròn tiếp xúc với cả ba cạnh đó. Khác với trọng tâm, tâm đường tròn nội tiếp liên quan đến các góc của tam giác và tính chất chia đôi góc của đường phân giác.

Tâm đường tròn ngoại tiếp là giao điểm của ba đường trung trực của tam giác. Điểm này cách đều ba đỉnh của tam giác và là tâm của đường tròn đi qua cả ba đỉnh đó. Vị trí của tâm đường tròn ngoại tiếp cũng phụ thuộc vào dạng tam giác, tương tự như trực tâm. Trong tam giác đều, bốn điểm đặc biệt này (trọng tâm, trực tâm, tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp) trùng nhau. Tuy nhiên, trong các tam giác khác, chúng thường phân biệt, tạo nên sự đa dạng và thú vị trong hình học tam giác.

Bạn đã biết giao điểm của ba đường trung tuyến là trọng tâm tam giác. Vậy còn tâm đường tròn nội tiếp tam giác thì sao? Khám phá ngay tâm đường tròn nội tiếp có gì đặc biệt!

Mối liên hệ giữa giao điểm đường trung tuyến và trọng tâm vật lý của tam giác

Giao điểm của ba đường trung tuyến trong một tam giác, hay còn gọi là trọng tâm tam giác, không chỉ là một khái niệm hình học mà còn có mối liên hệ mật thiết với trọng tâm vật lý của một tam giác đồng chất. Nói cách khác, nếu bạn cắt một miếng bìa cứng hình tam giác đồng chất (tức là có mật độ vật chất đồng đều), thì điểm mà bạn có thể đặt ngón tay vào để giữ miếng bìa thăng bằng hoàn hảo chính là giao điểm đường trung tuyến. Điều này cho thấy sự thống nhất giữa lý thuyết hình học và thực tế vật lý.

Thực tế, trọng tâm vật lý của một vật thể là điểm mà tại đó trọng lực tác dụng lên vật thể có thể được coi là tập trung. Đối với một tam giác đồng chất, điểm này trùng với giao điểm của các đường trung tuyến. Điều này có thể được chứng minh bằng các nguyên lý vật lý, đặc biệt là lý thuyết về mômen lực. Mỗi đường trung tuyến chia tam giác thành hai phần có diện tích bằng nhau. Do đó, nếu chúng ta tưởng tượng mỗi phần có trọng lượng bằng nhau, thì trọng tâm vật lý phải nằm trên đường trung tuyến đó. Vì cả ba đường trung tuyến đều cắt nhau tại một điểm, điểm đó phải là trọng tâm vật lý của tam giác.

Để làm rõ hơn, chúng ta có thể hình dung như sau: khi treo tam giác tại trọng tâm của nó, tam giác sẽ cân bằng hoàn hảo. Điều này là do tổng mômen lực tác dụng lên tam giác tại điểm treo bằng không. Các lực trọng trường tác dụng lên từng phần nhỏ của tam giác được cân bằng bởi lực phản lực tại điểm treo, và điểm cân bằng này chính là giao điểm ba đường trung tuyến. Ứng dụng này không chỉ thú vị về mặt lý thuyết mà còn có nhiều ứng dụng thực tế trong kỹ thuật và xây dựng, giúp xác định điểm cân bằng cho các cấu trúc hình tam giác.