Hình Bình Hành Có 2 Cạnh Liên Tiếp Bằng Nhau Là Hình Gì? [Giải Đáp 2025]

Hiểu rõ về hình bình hành và các biến thể của nó, đặc biệt khi hai cạnh liên tiếp bằng nhau, không chỉ là kiến thức toán học cơ bản mà còn là nền tảng để giải quyết nhiều bài toán hình học phức tạp. Vậy, trong thế giới hình học, hình bình hành có hai cạnh liên tiếp bằng nhau là hình gì? Bài viết này thuộc chuyên mục Hỏi Đáp, sẽ đi sâu vào khám phá bản chất của hình bình hành đặc biệt này, làm rõ mối liên hệ giữa nó với hình thoi, hình chữ nhật, và hình vuông. Chúng ta sẽ cùng nhau phân tích định nghĩa, tính chất, và các dấu hiệu nhận biết quan trọng, giúp bạn dễ dàng giải quyết các bài tập và ứng dụng kiến thức này vào thực tế.

Hình bình hành có hai cạnh liên tiếp bằng nhau: Đó là hình gì?

Trong thế giới hình học đa dạng, câu hỏi hình bình hành có hai cạnh liên tiếp bằng nhau là hình gì thường được đặt ra. Câu trả lời chính xác là hình bình hành đó chính là hình thoi. Điều này xuất phát từ định nghĩa và tính chất đặc biệt của hình thoi so với các hình tứ giác khác.

Hình thoi không chỉ là một hình bình hành đặc biệt mà còn sở hữu những thuộc tính riêng biệt. Điểm nổi bật của hình thoi là tất cả bốn cạnh của nó đều có độ dài bằng nhau. Điều này đồng nghĩa với việc nếu một hình bình hành có hai cạnh liên tiếp bằng nhau, thì hai cạnh đối diện của nó cũng bằng nhau (tính chất của hình bình hành), và do đó, cả bốn cạnh đều bằng nhau, đủ điều kiện để được gọi là hình thoi.

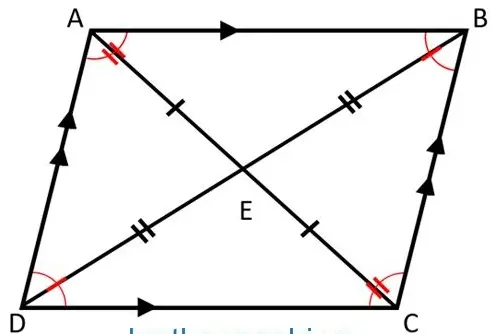
Để hiểu rõ hơn, chúng ta có thể hình dung một hình bình hành ABCD. Nếu AB = BC (hai cạnh liên tiếp bằng nhau), thì theo tính chất hình bình hành, AB = CD và BC = AD. Từ đó suy ra AB = BC = CD = AD, khẳng định ABCD là hình thoi. Như vậy, dấu hiệu nhận biết này không chỉ giúp ta xác định hình thoi một cách nhanh chóng mà còn làm nổi bật mối liên hệ giữa hình bình hành và hình thoi trong hình học.

Dấu hiệu nhận biết hình thoi nhanh chóng và chính xác

Để xác định một tứ giác có phải là hình thoi hay không một cách nhanh chóng và chính xác, chúng ta cần nắm vững các dấu hiệu nhận biết. Bài viết này sẽ cung cấp cho bạn những dấu hiệu nhận biết hình thoi đơn giản, dễ hiểu và hiệu quả nhất, giúp bạn không còn nhầm lẫn hình thoi với các hình tứ giác khác, đặc biệt là khi bài toán liên quan đến hình bình hành có 2 cạnh liên tiếp bằng nhau.

Một tứ giác được coi là hình thoi nếu nó thỏa mãn một trong các điều kiện sau:

• Tứ giác có bốn cạnh bằng nhau: Đây là dấu hiệu cơ bản nhất. Nếu bạn đo được bốn cạnh của một tứ giác và thấy chúng có độ dài bằng nhau, thì đó chắc chắn là hình thoi. Ví dụ: Tứ giác ABCD có AB = BC = CD = DA thì ABCD là hình thoi.

• Hình bình hành có hai cạnh kề bằng nhau: Nếu một tứ giác là hình bình hành và bạn xác định được hai cạnh kề của nó (hai cạnh có chung một đỉnh) có độ dài bằng nhau, thì tứ giác đó là hình thoi. Ví dụ: Hình bình hành EFGH có EF = FG thì EFGH là hình thoi. Đây cũng chính là câu trả lời trực tiếp nhất cho câu hỏi “hình bình hành có 2 cạnh liên tiếp bằng nhau là hình gì?”.

• Hình bình hành có hai đường chéo vuông góc với nhau: Nếu một tứ giác là hình bình hành và bạn chứng minh được hai đường chéo của nó cắt nhau tại một góc vuông, thì tứ giác đó là hình thoi. Ví dụ: Hình bình hành MNPQ có MP ⊥ NQ thì MNPQ là hình thoi.

• Hình bình hành có một đường chéo là đường phân giác của một góc: Nếu một tứ giác là hình bình hành và một trong hai đường chéo của nó chia một góc của hình bình hành thành hai góc bằng nhau, thì tứ giác đó là hình thoi. Ví dụ: Hình bình hành RSTU có RT là đường phân giác của góc R thì RSTU là hình thoi.

Nắm vững những dấu hiệu trên sẽ giúp bạn dễ dàng nhận biết hình thoi trong các bài toán hình học và ứng dụng thực tế. Hãy luôn ghi nhớ rằng, hình thoi vừa mang những đặc điểm của hình bình hành, vừa có những tính chất riêng biệt tạo nên sự khác biệt của nó.

Định nghĩa và các tính chất quan trọng của hình thoi bạn cần biết

Để hiểu rõ về hình bình hành có hai cạnh liên tiếp bằng nhau, điều quan trọng là phải nắm vững định nghĩa và các tính chất cơ bản của hình thoi. Hình thoi không chỉ là một hình tứ giác đặc biệt mà còn sở hữu nhiều tính chất hình học thú vị, đóng vai trò quan trọng trong việc giải quyết các bài toán liên quan.

Vậy, hình thoi là gì?

Hình thoi là một hình tứ giác có bốn cạnh bằng nhau. Nói cách khác, hình thoi là một trường hợp đặc biệt của hình bình hành, trong đó hai cạnh kề nhau có độ dài bằng nhau. Hình thoi có những đặc điểm trực quan, dễ nhận biết, và được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống.

Các tính chất quan trọng của hình thoi bạn cần nắm vững:

• Tính chất về cạnh: Đây là tính chất cơ bản nhất, hình thoi có bốn cạnh bằng nhau. Ví dụ, nếu một hình thoi ABCD có cạnh AB = 5cm, thì các cạnh BC, CD, DA cũng phải bằng 5cm.
• Tính chất về góc:
  • Các cạnh đối của hình thoi song song với nhau, điều này cũng đồng nghĩa với việc các góc đối bằng nhau. Ví dụ, góc A bằng góc C, góc B bằng góc D.
  • Hai đường chéo của hình thoi là các đường phân giác của các góc của hình thoi. Ví dụ, đường chéo AC chia góc A và góc C thành hai góc bằng nhau.
• Tính chất về đường chéo:
  • Hai đường chéo của hình thoi vuông góc với nhau tại trung điểm của mỗi đường. Ví dụ, nếu hai đường chéo AC và BD cắt nhau tại O, thì AO = OC, BO = OD và góc AOB = 90 độ.
  • Hai đường chéo của hình thoi cắt nhau tại trung điểm mỗi đường. Điều này có nghĩa là, giao điểm của hai đường chéo chia mỗi đường chéo thành hai đoạn bằng nhau.

Hiểu rõ các tính chất này sẽ giúp bạn dễ dàng nhận biết và giải quyết các bài tập liên quan đến hình thoi. Những tính chất này còn là nền tảng để so sánh hình thoi với các hình tứ giác đặc biệt khác như hình vuông, hình chữ nhật và hình bình hành, qua đó làm nổi bật những điểm khác biệt và mối liên hệ giữa chúng.

So sánh hình thoi với các hình tứ giác đặc biệt khác: Hình vuông, hình chữ nhật, hình bình hành

Để hiểu rõ hơn về hình thoi, việc so sánh nó với các hình tứ giác đặc biệt khác như hình vuông, hình chữ nhật và hình bình hành là vô cùng quan trọng, giúp chúng ta phân biệt được các đặc điểm riêng biệt của từng hình và nắm vững kiến thức về hình học. Việc so sánh này sẽ làm rõ khái niệm ” hình bình hành có hai cạnh liên tiếp bằng nhau là hình gì” một cách trực quan và dễ hiểu.

Để có cái nhìn tổng quan, chúng ta sẽ đi sâu vào so sánh hình thoi với từng hình tứ giác đặc biệt, tập trung vào các yếu tố như cạnh, góc, đường chéo và tính đối xứng.

Đặc điểm	Hình thoi	Hình vuông	Hình chữ nhật	Hình bình hành
Cạnh	Bốn cạnh bằng nhau	Bốn cạnh bằng nhau	Hai cặp cạnh đối bằng nhau	Hai cặp cạnh đối bằng nhau
Góc	Các góc đối bằng nhau, không nhất thiết vuông	Bốn góc vuông	Bốn góc vuông	Các góc đối bằng nhau, không nhất thiết vuông
Đường chéo	Vuông góc và cắt nhau tại trung điểm mỗi đường	Vuông góc, bằng nhau và cắt nhau tại trung điểm	Bằng nhau và cắt nhau tại trung điểm	Cắt nhau tại trung điểm
Đối xứng	Có hai trục đối xứng	Có bốn trục đối xứng	Có hai trục đối xứng	Không có trục đối xứng (trừ trường hợp đặc biệt)

• Hình vuông: Hình vuông là một trường hợp đặc biệt của hình thoi, khi nó vừa có bốn cạnh bằng nhau (như hình thoi), vừa có bốn góc vuông. Nói cách khác, hình vuông là hình thoi có một góc vuông. Do đó, mọi hình vuông đều là hình thoi, nhưng không phải hình thoi nào cũng là hình vuông.

• Hình chữ nhật: Hình chữ nhật có các góc vuông, nhưng các cạnh không nhất thiết phải bằng nhau như hình thoi. Hình chữ nhật có hai cặp cạnh đối diện bằng nhau, trong khi hình thoi có bốn cạnh bằng nhau.

• Hình bình hành: Hình bình hành có các cạnh đối diện song song và bằng nhau, các góc đối diện bằng nhau, nhưng không nhất thiết có cạnh bằng nhau hoặc góc vuông như hình thoi. Hình thoi là một trường hợp đặc biệt của hình bình hành, khi có thêm điều kiện hai cạnh kề bằng nhau. Như vậy, hình bình hành có hai cạnh liên tiếp bằng nhau chính là hình thoi.

Qua sự so sánh này, hy vọng bạn đã hiểu rõ hơn về hình thoi và cách phân biệt nó với các hình tứ giác đặc biệt khác.

Các công thức tính toán liên quan đến hình thoi: Diện tích, chu vi, đường cao

Hình thoi, một dạng hình bình hành có hai cạnh liên tiếp bằng nhau, không chỉ thu hút bởi vẻ ngoài cân đối mà còn bởi những công thức tính toán diện tích, chu vi và đường cao đặc trưng. Việc nắm vững các công thức này giúp bạn dễ dàng giải quyết các bài toán liên quan đến hình thoi, đồng thời ứng dụng chúng vào thực tiễn một cách hiệu quả.

Để tính toán các thông số của hình thoi, chúng ta cần nắm rõ các yếu tố cấu thành. Chu vi hình thoi được tính dựa trên độ dài cạnh, trong khi diện tích hình thoi có thể được tính thông qua độ dài hai đường chéo hoặc cạnh và đường cao. Hiểu rõ mối liên hệ giữa các yếu tố này sẽ giúp bạn linh hoạt áp dụng công thức phù hợp trong từng trường hợp cụ thể.

Dưới đây là các công thức chi tiết giúp bạn tính toán một cách chính xác:

• Tính diện tích hình thoi khi biết độ dài hai đường chéo: Diện tích hình thoi bằng nửa tích độ dài hai đường chéo. Công thức: S = (d1 * d2) / 2, trong đó d1 và d2 là độ dài hai đường chéo. Ví dụ, nếu một hình thoi có hai đường chéo lần lượt là 6cm và 8cm, diện tích của nó sẽ là (6 * 8) / 2 = 24cm².

• Tính diện tích hình thoi khi biết cạnh và đường cao: Diện tích hình thoi bằng tích của độ dài cạnh và đường cao tương ứng. Công thức: S = a * h, trong đó a là độ dài cạnh và h là độ dài đường cao. Ví dụ, nếu hình thoi có cạnh dài 5cm và đường cao tương ứng là 4cm, diện tích của nó sẽ là 5 * 4 = 20cm².

• Tính chu vi hình thoi: Chu vi hình thoi bằng bốn lần độ dài cạnh. Công thức: P = 4 * a, trong đó a là độ dài cạnh. Ví dụ, nếu một hình thoi có cạnh dài 7cm, chu vi của nó sẽ là 4 * 7 = 28cm.

Hiểu và áp dụng thành thạo các công thức này sẽ giúp bạn giải quyết các bài toán liên quan đến hình thoi một cách nhanh chóng và chính xác.

Ứng dụng thực tế của hình thoi trong đời sống và toán học

Hình thoi, một dạng đặc biệt của hình bình hành có hai cạnh liên tiếp bằng nhau, không chỉ là một khái niệm hình học trừu tượng mà còn có nhiều ứng dụng thiết thực trong đời sống và toán học. Từ kiến trúc, thiết kế đến các bài toán thực tế, hình thoi đóng vai trò quan trọng.

Trong kiến trúc và xây dựng, hình thoi được sử dụng rộng rãi để tạo ra các hoa văn trang trí độc đáo, các cấu trúc chịu lực hiệu quả. Chúng ta có thể dễ dàng nhận thấy hình thoi trong các ô cửa sổ, họa tiết trên sàn nhà, mái ngói, hay thậm chí trong thiết kế cầu đường. Ví dụ, các họa tiết hình thoi trên sàn nhà không chỉ mang tính thẩm mỹ mà còn giúp tăng độ ma sát, chống trơn trượt. Cấu trúc dạng hình thoi thường được sử dụng trong các giàn thép, khung mái vì khả năng phân bổ lực đều, giúp tăng độ bền vững cho công trình.

Trong thiết kế và trang trí, hình thoi mang đến vẻ đẹp cân đối, hài hòa, và tinh tế. Chúng ta có thể thấy hình thoi xuất hiện trong các mẫu gạch lát, giấy dán tường, đồ trang sức, và nhiều vật dụng trang trí khác. Họa tiết hình thoi được ứng dụng trong thiết kế logo, tạo nên sự độc đáo và dễ nhận diện cho thương hiệu. Ví dụ, nhiều thương hiệu thời trang nổi tiếng sử dụng họa tiết hình thoi trong các sản phẩm của mình, tạo nên dấu ấn riêng biệt.

Trong toán học, hình thoi là một đối tượng nghiên cứu quan trọng, liên quan đến nhiều khái niệm và định lý khác. Việc nghiên cứu hình thoi giúp học sinh, sinh viên rèn luyện tư duy logic, khả năng giải quyết vấn đề, và ứng dụng kiến thức vào thực tế. Các bài toán liên quan đến hình thoi thường xuất hiện trong các kỳ thi, giúp đánh giá khả năng tư duy hình học của học sinh. Ví dụ, bài toán tính diện tích hình thoi khi biết độ dài hai đường chéo là một dạng bài tập cơ bản nhưng quan trọng.

Ứng dụng khác của hình thoi có thể thấy trong các trò chơi dân gian như thả diều, làm đèn lồng. Hình dáng hình thoi giúp diều bay cao và ổn định hơn. Ngoài ra, trong lĩnh vực khoa học vật liệu, các cấu trúc nano có dạng hình thoi được nghiên cứu để ứng dụng trong các thiết bị điện tử, cảm biến, và vật liệu siêu bền. Nghiên cứu về hình thoi và các tính chất của nó vẫn tiếp tục được phát triển, mở ra nhiều ứng dụng tiềm năng trong tương lai.

Các bài tập vận dụng về hình thoi từ cơ bản đến nâng cao (có đáp án)

Để nắm vững kiến thức về hình thoi và hình bình hành có 2 cạnh liên tiếp bằng nhau, việc luyện tập giải các bài tập vận dụng là vô cùng quan trọng. Phần này sẽ cung cấp một loạt bài tập về hình thoi, từ cơ bản đến nâng cao, kèm theo đáp án chi tiết, giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán hình học một cách hiệu quả nhất.

Các bài tập sẽ bao gồm nhiều dạng khác nhau, từ việc nhận biết dấu hiệu hình thoi đến tính toán diện tích, chu vi và các yếu tố liên quan khác. Chúng ta sẽ đi từ những bài tập đơn giản, giúp bạn làm quen với các khái niệm cơ bản, đến những bài tập phức tạp hơn, đòi hỏi sự vận dụng linh hoạt các tính chất và công thức.

Bài tập cơ bản:

1. Cho hình bình hành ABCD có AB = BC. Chứng minh rằng ABCD là hình thoi.

   • Đáp án: Vì ABCD là hình bình hành và AB = BC nên ABCD là hình thoi (dấu hiệu nhận biết).

2. Cho hình thoi MNPQ có cạnh MN = 5cm. Tính chu vi của hình thoi MNPQ.

   • Đáp án: Chu vi hình thoi MNPQ là 4 MN = 4 5cm = 20cm.

3. Cho hình thoi EFGH có hai đường chéo EG và FH cắt nhau tại O. Biết EG = 8cm, FH = 6cm. Tính diện tích hình thoi EFGH.

   • Đáp án: Diện tích hình thoi EFGH là (1/2) EG FH = (1/2) 8cm 6cm = 24cm².

Bài tập nâng cao:

1. Cho tam giác ABC cân tại A. Gọi D là trung điểm của BC. Qua D vẽ đường thẳng song song với AB cắt AC tại E, và vẽ đường thẳng song song với AC cắt AB tại F. Chứng minh rằng AEDF là hình thoi.

   • Gợi ý: Chứng minh AEDF là hình bình hành có hai cạnh kề bằng nhau.

2. Cho hình thoi ABCD có góc A = 60°. Chứng minh rằng tam giác ABD là tam giác đều.

   • Gợi ý: Sử dụng tính chất các cạnh của hình thoi bằng nhau và tổng các góc trong tam giác.

3. Một mảnh đất hình tứ giác ABCD có AB = BC = CD = DA = 5m và AC = 8m.

   • a) Chứng minh rằng ABCD là hình thoi.

   • b) Tính diện tích mảnh đất ABCD.

   • Gợi ý:

     • a) Dựa vào định nghĩa hình thoi.
     • b) Chia hình thoi thành hai tam giác bằng nhau và sử dụng công thức Heron để tính diện tích tam giác.

Hy vọng, với các bài tập hình thoi này và các bài tập tương tự, bạn sẽ tự tin hơn trong việc giải quyết các bài toán liên quan và hiểu rõ hơn về định nghĩa hình thoi cũng như các tính chất hình thoi quan trọng. Chúc bạn thành công!